In my previous blog, MachineX: Two parts of Association Rule Learning, we discussed that there are two parts in performing association rule learning, namely, frequent itemset generation and rule generation. In this blog, we are going to talk about one of the algorithms for frequent itemset generation, viz., Apriori algorithm.
The Apriori Principle
Apriori algorithm uses the support measure to eliminate the itemsets with low support. The use of support for pruning candidate itemsets is guided by the following principle –
If an itemset is frequent, then all of its subsets must also be frequent.
The above principle is known as The Apriori Principle.
I have already explained what support is in one of my previous blogs, MachineX: Layman guide to Association Rule Learning. To recall, support tells us that how frequent is an item, or an itemset, in all of the dataset.
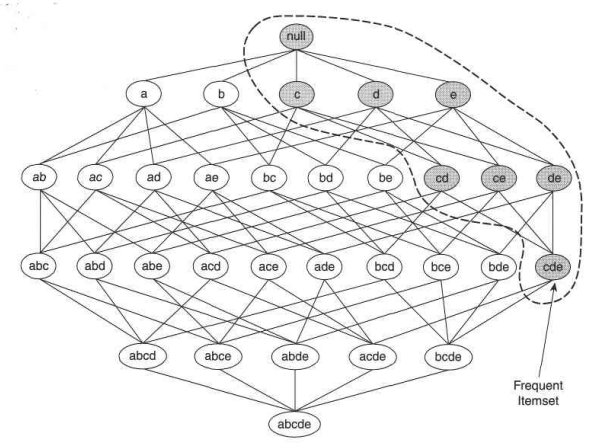
Consider the item lattice shown above. Suppose {c, d, e} is a frequent itemset. Then, all the transactions that contain {c, d, e} also contain {c, d}, {c, e}, {e, d}, {c}, {d} and {e}. So, these items also have to be frequent for {c, d, e} to be frequent. Conversely, if an itemset, suppose {a, b} is infrequent, then all of its supersets have to be infrequent too, which means that all the transactions, for example, {a, b, c}, {a, b, d}, etc. have to be infrequent too. So, all the transactions containing {a, b} can be immediately pruned. This strategy of trimming the exponential search space based on the support measure is known as support-based pruning. Such a pruning strategy is made possible by a key property of the support measure, that is, the support for an itemset never exceeds the support
for its subsets. This property is also known as the anti-monotone property of the support measure.
Frequent Itemset Generation in Apriori Algorithm
Apriori algorithm uses support-based pruning to control the exponential growth of the candidate itemsets. Let’s understand this with an example.

Let’s suppose the minimum threshold value is 3. So, the itemsets with support value of 3 or greater than 3 would be considered frequent. In the 1-itemset, the greyed out values are the infrequent itemsets and rest are frequent. So, first of all, all the 1-itemsets in the given dataset is listed with their frequencies as shown in the 1-itemset table in the above figure. Then, 2-itemset table is generated using only those items of the 1-itemset table which are frequent, i.e., have their support values greater than or equal to 3. In this way, we only get 6 2-itemset. If pruning wasn’t done, we would have got 15 2-itemsets at this step. Further, we can eliminate all the 2-itemsets with support less than 3. After doing that, we get 4 2-itemsets using which we generate 3-itemsets, which is ultimately just 1. If no pruning was performed we would have got a total of 41 itemsets, but after pruning, we get only 13 itemsets, a significant reduction!!
But then, why is it not being used?
Well, even after being so simple and clear, it has some weaknesses. If the 1-itemset comes out to be very large, for ex. 104, then the 2-itemset candidate sets would be more than 107. Moreover, for a dataset with a large number of frequent items or with a low support value, the candidate itemsets will always be very large. These large datasets require a lot of memory to be stored in. Further, apriori algorithm also scans the database multiple times to calculate the frequency of the itemsets in k-itemset. So, apriori algorithm turns out to be very slow and inefficient, especially when memory capacity is limited and the number of transactions is large.
In my next blog, we are going to talk about one of the alternatives of apriori algorithm, viz., FP-Growth algorithm, which is a significant improvement over apriori. So, stay tuned!
References –
- Introduction to data mining by Pang-Ning Tan, Michael Steinbach and Vipin Kumar
- “An Improvement on apriori algorithm” paper by Mohammed Al-Maolegi and Bassam Arkok



2 thoughts on “MachineX: Why no one uses apriori algorithm for association rule learning?3 min read”
Comments are closed.